LINUX内核数据结构-RBTREE
1.前言
这是linux内核数据结构的第三篇,前两篇分别讲了list和hashtable,有不熟悉的小伙伴可以移步参观下。
本篇我们将研究下rbtree的实现。
rbtree是一个高效的平衡二叉树,在我们不断插入节点的过程中,他会根据二叉树左右子树的深度情况不断地对两边进行调整,从而保证左右子树的平衡,进而保证良好的查找性能。另外,rbtree还是有序的,这一点也非常重要。
rbtree的实现在linux内核中分散在三个文件中,分别是rbtree_augmented.h、rbtree.h、rbtree.c,感兴趣的话可移步参考。
特别提醒一点,rbtree的复杂程度和前面我们研究的list、hashtable不是一个量级的,请做好心理准备。另外,本篇文章的完整代码已经上传至我的github了,供您参考。
2.初始化
2.1 定义结构体
按照老规矩,先定义结构体:
struct task_node_t
{
int task_id;
struct rb_node node;
};我们定义一个表示任务的结构体,包含了一个task_id字段和内嵌的rbree节点字段(如果不知道这个节点元素是干啥的,建议回头翻翻前面讲list和hashtable的文章)。
我们的基本需求是,将task按照task_id从小到大排序。
rbtree的普通节点和根节点的定义如下:
// copy from kernel/include/linux/rbtree.h
struct rb_node {
unsigned long __rb_parent_color;
struct rb_node *rb_right;
struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));
struct rb_root {
struct rb_node *rb_node;
};可以看到:
- 根节点结构体只包含一个指向普通节点的指针
- 普通节点结构体包含了指向左右两个子树的指针rb_left和rb_right
- 普通节点结构体的__rb_parent_color字段其实是个复合字段,可以同时表示父节点指针和本节点的颜色
2.2 __rb_parent_color
__rb_parent_color的最后1位是表示本节点的颜色的,相关的代码段如下:
// copy from kernel/include/linux/rbtree_augmented.h
#define RB_RED 0
#define RB_BLACK 1
#define __rb_color(pc) ((pc) & 1)
#define __rb_is_black(pc) __rb_color(pc)
#define __rb_is_red(pc) (!__rb_color(pc))
#define rb_is_red(rb) __rb_is_red((rb)->__rb_parent_color)
#define rb_is_black(rb) __rb_is_black((rb)->__rb_parent_color)其实是取了__rb_parent_color的最后1位,为1表示黑节点,为0表示红节点。
取父节点地址的操作是:
#define rb_parent(r) ((struct rb_node *)((r)->__rb_parent_color & ~3))3的二进制表示是0000…000011,取反后进行与操作,即可去掉尾部的表示节点颜色的位。
看到这里感觉有点懵,这是什么操作?还能这样玩?
这里其实有一个精巧的设计。
我们注意到前面定义rb_node时,指定了一个字节对齐操作。在32位系统上,是按照4字节对齐,在64位系统上,是按照8字节对齐的。这就意味着,rb_node结构体的指针数值,后2位或3位是0。与其舍弃不用,不如用来存放节点的颜色。一来废弃的比特位用上了, 二来还能避免定义新的变量表示节点颜色,浪费内存。
回到前面的求父节点地址的操作,这里其实是空了两个比特位,这样的话,即使是在32位系统上也能正常运行。
与__rb_parent_color相关的还有两个操作,一个是求红节点父节点的操作:
static inline struct rb_node *rb_red_parent(struct rb_node *red)
{
return (struct rb_node *)red->__rb_parent_color;
}
由于红节点的__rb_parent_color表示颜色的位是0,而字节对齐又保证了倒数第二位也是0,因此这里直接做个强转就行了。
另外一个操作是设置节点颜色的操作:
static inline void rb_set_parent_color(struct rb_node *rb,
struct rb_node *p, int color)
{
rb->__rb_parent_color = (unsigned long)p | color;
}color参数传的是上面的RB_BLACK或者RB_RED宏,只占一个比特位,因此这里直接与一下就行了。
2.3 定义rbtree
定义rbtree的代码非常简单:
#define RB_ROOT (struct rb_root) { NULL, }
struct rb_root task_tree = RB_ROOT;就是定义一个根节点,把他唯一的元素rb_node指针置空即可。
3.插入
3.1 测试代码
测试代码如下:
struct rb_root task_tree = RB_ROOT;
struct task_node_t *p_task;
//插入100个元素
for (i=0; i < 100; i++)
{
p_task = (struct task_node_t *)malloc(sizeof(struct task_node_t));
p_task->task_id = 100 -1 - i;
task_insert(&task_tree, p_task);
}插入100个元素,把他的task_id字段降序设置一下(因为我们想要的功能是按照task_id从小到大排列,降序设置的话可以测试下排序功能是否生效),然后调用task_insert函数把节点插入到rbtree里。
3.2 task_insert函数
这个task_insert函数是我们自己实现的,linux内核的rbtree没有提供通用的插入函数,因此需要我们自己实现。
我们的task_insert函数代码如下:
int task_insert(struct rb_root *p_root, struct task_node_t *p_task)
{
struct rb_node **p_new = &p_root->rb_node;
struct rb_node *p_parent = NULL;
struct task_node_t *p_this;
while (*p_new)
{
p_this = container_of(*p_new, struct task_node_t, node);
p_parent = *p_new;
if (p_task->task_id < p_this->task_id)
p_new = &((*p_new)->rb_left);
else if (p_task->task_id > p_this->task_id)
p_new = &((*p_new)->rb_right);
else
return 0;
}
rb_link_node(&p_task->node, p_parent, p_new);
rb_insert_color(&p_task->node, p_root);
return 1;
}3.3 寻找插入位置
我们要实现的功能,是把p_task插入到p_root里面,返回值表示是否进行了插入。
插入的时候要在子树中寻找插入位置,因此定义了三个指针:
- p_new表示要插入的位置,一开始是指向根节点的rb_node,既第一个普通节点的
- p_parent指向要插入的位置的父节点,初始化为空指针
- p_this是p_new所指节点的容器结构体指针,在我们的例子中,是task_node_t指针
然后开始插入操作。
这是个循环的过程,他会根据当前所指节点的task_id和我们要插入的节点的task_id的大小选择插入位置,小的放在左子树,大的放在右子树,相等则直接返回,不再插入。
注意上述按照大小排序选择以及相等返回的控制都是由我们自己做的,如果有需要,我们完全可以实现一个左大右小的排序规则,或者task_id相等则替换的插入规则,或者把多个字段综合起来判断大小的规则。
上面的节点插入操作,找到了两个指针,一个是要插入节点的父节点p_parent,一个是p_parent对应子树的指针的指针p_new。即上述过程只是找到了要插入的位置,并没有把节点真正的插入。
3.4 插入节点
真正的插入操作要调用下面的函数:
static inline void rb_link_node(struct rb_node *node, struct rb_node *parent,
struct rb_node **rb_link)
{
node->__rb_parent_color = (unsigned long)parent;
node->rb_left = node->rb_right = NULL;
*rb_link = node;
}为新节点设置父节点,初始化左右子树为空,把父节点的对应子树指向新节点。
3.5 节点调整
节点完成插入后,可能导致红黑树的定义被打破,因此需要进行变色和旋转,以使其满足红黑树的定义。
在我们的例子中,代码如下:
rb_insert_color(&p_task->node, p_root);rb_insert_color的实现如下:
static inline void dummy_rotate(struct rb_node *old, struct rb_node *new) {}
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
__rb_insert(node, root, dummy_rotate);
}他调用了__rb_insert函数,传入了一个旋转函数(不过是空的)。
__rb_insert这个函数比较复杂,为了顺利理解他,我们需要复习一下红黑树的规则。
a) 红黑树规则
一个红黑树需要满足如下五个条件:
- 普通节点是红色或黑色
- 根节点是黑色
- 所有的叶子节点都是黑色的(叶子是NIL节点)
- 每个红色节点必须有两个黑色的子节点(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点

这个规则比较复杂,我们简单解释一下:
- 上面说的叶子节点并不是真正的节点,这个规则的意思是把叶子节点的空子树视为黑色节点(如上图)
- 规则1和规则3是一定满足的,他其实只是个约定,我们直接遵照即可
- 规则4只有在增加红色节点、把黑色节点设为红色、或做旋转时才有可能打破
- 规则5只有在增加黑色节点、把红色节点设为黑色、或做旋转时才有可能打破
另外,我们可以约定,新插入的节点是红色的。因为如果约定新插入的节点是黑色的话,会导致规则5失效,这是很难调整的。但是如果约定新插入节点是红色的,那么对规则5其实没有影响,只需要处理规则4的连续红色节点冲突即可,我们需要处理的情形就会大大减少。
b)分情形说明
为了说明几种情形,我们先对节点的命名作出约定:
- New代表新插入的节点
- Parent代表新插入节点的父节点
- Grand parent代表插入节点的父节点的父节点
- Uncle代表新插入节点的父节点的兄弟节点
情形1:N位于树的根上,没有父节点。
此时只打破了规则2,因此我们把根节点设置为黑色即可,同时规则4和5也没有被打破,代码如下(根节点的父节点指针为NULL,自己的颜色是黑色):
struct rb_node *parent = rb_red_parent(node);
while (1) {
/*
* Loop invariant: node is red.
*/
if (!parent) {
/*
* The inserted node is root. Either this is the
* first node, or we recursed at Case 1 below and
* are no longer violating 4).
*/
rb_set_parent_color(node, NULL, RB_BLACK);
break;
}情形2:新节点的父节P是黑色的
此时插入新节点不影响任何任何一个规则,因此无需调整直接插入即可。
情形3:新节点的父亲P和叔父U都是红色的
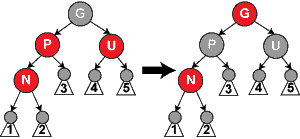
在未调整前,根据规则4,祖父节点G一定是黑色的。
增加红色节点N后:
- 导致规则4被打破,因此需将节点P改成黑色的
- 为了保持N所在的链路上黑色节点数量不变,因此需将祖父节点改成红色的
- 同时为了保持叔父U所在节点的黑色节点数量不变,需要将叔父改成黑色的
- 祖父G可能是根节点,因此其变成红色后可能导致规则2失效,需要以祖父G为新节点递归执行上述过程
代码如下:
- 小写字母代表红色节点,大写字母代表黑色节点
- rb_set_parent_color是同时设置父节点的指针和本节点的颜色
- 把第一个参数的父节点指针设置为第二个参数
- 把第一个参数的颜色设置为第三个参数
- tmp指向叔父节点U
- node指向新节点n
- 在末尾的continue之前,它把node指向了祖父节点G,进入下一次循环
/*
* Case 1 - node's uncle is red (color flips).
*
* G g
* / \ / \
* p u --> P U
* / /
* n n
*
* However, since g's parent might be red, and
* 4) does not allow this, we need to recurse
* at g.
*/
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue;情形4:新节点的父亲P是红色的,叔父U都是黑色的(或没有),新节点位于其父亲节点的右子树上

在未调整前,根据规则4,祖父节点G一定是黑色的。
处理这个情形,要么改颜色,要么旋转。
先看改颜色的方案:我们可以效仿情形3把P改成黑色,然后由于N所在链路上多了个黑节点,因此需将祖父G改成红色,但是此时叔父节点所在的链路上会少一个黑色节点,这就很难处理了。此路不通。
那就只能做旋转了:因为旋转是不改变颜色总量,只改变颜色分布的。上图左侧这种树形是不利于我们进行接下来的旋转的,因此我们先将上图左边的树形调整成右边的树形,使其符合情形5的条件,注意上述调整后的树形依然不符合规则4,我们继续运行情形5的处理过程来修正这一点。
在本情形下,我们只需要对祖父节点P进行一次左旋(N成为新的父节点,P成为N的左子树,N原先的左子树成为P的右子树)即可。
代码如下:
- node指向的是新节点N
- 注意下面的两个rb_set_parent_color的目的都是改变父指针,而非改变当前节点的颜色
- tmp指向的是新节点N的左子树,旋转后他成了父节点P的右子树,需要修改父节点指针
- 新节点N旋转后成了父亲节点P的父亲节点,需要修改父节点指针
- augment_rotate是个空实现,不做任何操作
- 最后更新指针,父节点指向原先的新节点,tmp指向原先的新节点的右子树
- 末尾没有break或continue,表明会继续进行下一种情形的处理
/*
* Case 2 - node's uncle is black and node is
* the parent's right child (left rotate at parent).
*
* G G
* / \ / \
* p U --> n U
* \ /
* n p
*
* This still leaves us in violation of 4), the
* continuation into Case 3 will fix that.
*/
tmp = node->rb_left;
parent->rb_right = tmp;
node->rb_left = parent;
if (tmp)
rb_set_parent_color(tmp, parent,
RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_right;情形5:新节点的父亲P是红色的,叔父U都是黑色的(或没有),新节点位于其父亲节点的左子树上
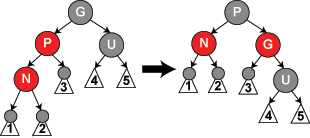
这种情况有可能是原生的,也有可能是由上述的情形4调整而来的。
这种情况下,改变节点颜色依然行不通(理由同情形4),因此只能做旋转,不改变颜色的总数量,只改变不同颜色分布的位置。
我们调整的目标是,把左边的连续两个红色节点分开(满足规则4),同时不改变右边的黑色节点总数(满足规则5)。
调整方法如下:
- 对P做一次右旋,把G变成P的右子树
- 然后对调P和G的颜色
代码如下:
- tmp指向的是父节点P的右子树
- 父节点P的右子树旋转后变成了G的左子树,颜色不变(仍为黑色)
- 父节点P变为根节点,右子树变成了祖父节点G
- 父节点P的颜色变成了黑色,祖父节点G的颜色变成了红色
- augment_rotate是个空实现,不做任何操作
- 末尾有个break,表明处理结束
/*
* Case 3 - node's uncle is black and node is
* the parent's left child (right rotate at gparent).
*
* G P
* / \ / \
* p U --> n g
* / \
* n U
*/
gparent->rb_left = tmp; /* == parent->rb_right */
parent->rb_right = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;4.搜索
搜索的测试代码如下:
//search
for(i=0;i<100;i++)
{
p_task = task_search(&task_tree, i);
printf("%d %d\n", i, p_task->task_id);
}与插入算法类似,搜索算法也需要我们自己实现:
struct task_node_t *task_search(struct rb_root *p_root, int task_id)
{
struct rb_node *p_node = p_root->rb_node;
struct task_node_t *p_task;
while (p_node)
{
p_task = container_of(p_node, typeof(*p_task), node);
if (task_id < p_task->task_id)
p_node = p_node->rb_left;
else if (task_id > p_task->task_id)
p_node = p_node->rb_right;
else
return p_task;
}
return NULL;
}这段代码跟插入的代码task_insert非常类似,我们不再重复解释。
运行效果如下:
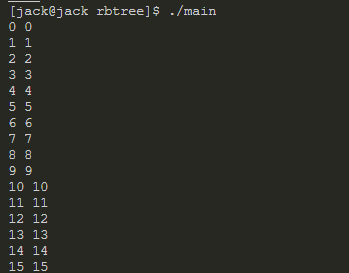
5.遍历
遍历的测试代码如下:
//遍历
struct rb_node *p_node;
for (p_node = rb_first(&task_tree); p_node; p_node = rb_next(p_node))
printf("task_id=%d\n", rb_entry(p_node, struct task_node_t, node)->task_id);运行效果如下:
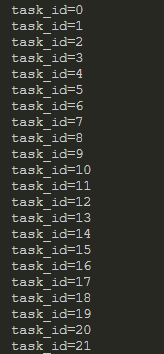
我们发现,虽然我们插入的时候是倒序插入的,但是遍历的时候自动变成正序了,我们的目的也达到了。
其中rbfirst的代码如下:
struct rb_node *rb_first(const struct rb_root *root)
{
struct rb_node *n;
n = root->rb_node;
if (!n)
return NULL;
while (n->rb_left)
n = n->rb_left;
return n;
}即先从左子树的叶子节点遍历。
rb_next代码如下:
struct rb_node *rb_next(const struct rb_node *node)
{
struct rb_node *parent;
if (RB_EMPTY_NODE(node))
return NULL;
/*
* If we have a right-hand child, go down and then left as far
* as we can.
*/
if (node->rb_right) {
node = node->rb_right;
while (node->rb_left)
node = node->rb_left;
return (struct rb_node *)node;
}
/*
* No right-hand children. Everything down and left is smaller than us,
* so any 'next' node must be in the general direction of our parent.
* Go up the tree; any time the ancestor is a right-hand child of its
* parent, keep going up. First time it's a left-hand child of its
* parent, said parent is our 'next' node.
*/
while ((parent = rb_parent(node)) && node == parent->rb_right)
node = parent;
return parent;
}求下一个节点的时候,自己肯定是没有左子树的,因此得先看看有没有右子树:
- 如果有的话取其左子树的叶子节点。
- 如果没有的话,说明当前节点包括其左右子树都已经遍历完了,需要往父节点走
- 如果自己是父节点的左子树,那么直接返回父节点即可
- 如果自己是父节点的右子树,说明父节点也遍历完了(遍历顺序是左子树、节点本身、右子树)需要再往上走一级
6.心得体会
6.1 Can I make it simple?
从list、hashtable到本篇文章的rbtree,我们不难发现linux内核数据结构的一个设计原则,即只实现必须实现的,用户能实现的就让用户去实现。
比如rbtree,linux内核仅实现了最核心的部分,像插入搜索查询这类功能都让用户去实现了。这也是linux内核能够保持精简高效的秘诀之一吧。
保持简单,但是把简单的事情做到极致。我们做任何软件,甚至做任何决策的时候都可以借鉴这一点。这个功能非得用这么复杂的方式实现么?这段代码可以再简单一点么?这件事情我必须做么?Can I make it simple?
6.2 问题降维能力
另一个体会是,这些算法大神和代码大神们总是能通过分析,发现一些隐藏的前提条件,从而把要做的事情不断地化简,最后变成一个规模又小,难度又低的问题,让普通人也能理解。
这就是问题降维能力,是一种高级能力。高手总是能把问题的规模和难度的等级不断降低,把复杂的事情不断化简,最后让普通人也能满足工作要求,参与到复杂的工作中去。